روز چهارشنبه ۱۹ اردیبهشتماه، دکتر حسین عبده تبریزی در پنجمین همایش ریاضیات و علوم انسانی که به همت دانشکدهی علوم ریاضی و رایانه و دانشکدهی اقتصاد دانشگاه علامهطباطبایی برگزار شده بود، شرکت کرد و سخنرانیای با عنوان ʺنقش ریاضیات در توسعهی علم مالیʺ ارائه نمود.
نشریهی اطلاعات بورس در شمارهی ۲۵۲ به تاریخ ۵ خردادماه، شرحی از صحبتهای دکتر عبده تبریزی در همایش ریاضیات و علوم انسانی را به چاپ رسانیده است.
متن این سخنرانی را اینجا بیابید.
نقش ریاضیات در توسعهی علم مالی
حسین عبده تبریزی*
۱. بحران مالی ۲۰۰۷ و مذمت ریاضیات و مخهای بازار[۱]
با وقوع بحران مالی ۲۰۰۷، عدهای ریاضیات و ریاضیدانان بازارهای سرمایه را متهم کردند که مدلهای پیچیده و محرمانه بکار بستهاند و این مدلسازیهای غلط زمینهساز وقوع بحران بوده است. البته، چنین حرفی از پایه غلط است، و به این میماند که ما رشتهی حسابداری و حسابداران را برای حسابسازی مقصر بدانیم.
۲. تأثیر متقابل توسعهی نظریهی مالی و ریاضیات
چگونه توسعهی نظریهی مالی بر ریاضیات تأثیر گذاشت و با توسعهی نظریهی مالی ریاضی، به نوبهی خود ریاضیات بر حوزهی مالی اثر گذاشت.
البته، مدلهای پیچیدهی ریاضی همیشه محور نظریهی مالی نبوده است. در طول دورهای بلند، مالی[۲] علمی توصیفی باقی ماند که تمرکزش بر مسائل قانونی و نهادها بود. نظریهی مالی چیزی غیر از مجموعهای از حکایتها، قواعد سرانگشتی و پسوپیشکردن اطلاعات حسابداری نبود. حداکثر تمرکز مدلهای ریاضی روی ارزش زمانی پول بود و پیچیدهترین ابزار تحلیل در آن زمان ارزش فعلی بود. در واقع کار کمّی باشلیهی[۳] ریاضیدان در سال ۱۹۰۰ هم حدود ۶۰ سال از چشم اقتصاددانان مخفی ماند.
من در سال ۱۳۵۳ در شروع اولین کلاسهای تدریس خود، وقتی درس مدیریت مالی (۱) ارائه میکردم، مباحث پایهای چون بودجهی نقدی، نقطهی سربسری، تحلیل صورتهای مالی (نسبتها)، و حداکثر بودجهبندی سرمایهای تدریس میشد؛ هیچ معلمی غیر از حسابداران در دسترس نبود. چند ماه بعد هم که برای دورهی دکترا به انگلستان رفتم، هنوز بحثهای کمی در عرصهی مالی فراتر از نظریهی مارکویتز نمیرفت.
علم مالی حتی در دههی ۷۰ قرن بیستم میلادی در عرصهی اجرا تا سر حد بودجهبندی سرمایهای میرفت. اگرچه مککالی[۴] در سال ۱۹۳۸ بحث دیرش[۵]، یعنی حساسیت قیمت قرضه به نرخ بهره، را طرح کرده بود، اما در اجرا تا چند دهه بعد از آن استفادهای نمیشد.
برای توضیح ریاضیات مالی در چنین نشستی طبعاً لازم نیست تعریفی از ریاضیات ارائه کنم. اما در مورد درک من از مالی، باید بگویم که هستهی اصلی بحث نظریهی مالی عبارت است از مطالعهی رفتار عوامل اقتصادی در تخصیص و بهرهبرداری از منابع در مکانها و زمانهای مختلف، و البته در محیط نامطمئن.
برای توضیح واکنش متقابل بین مدلهای ریاضی و حیطهی عمل مالی باید بگویم که زمان و عدمقطعیت عوامل اصلی است که بر رفتار مالی تأثیر میگذارد. پیچیدگی روابط متقابل این دو غالباً به ابزارهای تحلیلی پیچیدهای نیاز دارد که آثار این رابطهی متقابل را توضیح دهد. اینجاست که مدلهای ریاضی مالی نوین به کار میآید و شاهد بعضی از زیباترین کاربردهای نظریهی احتمالات و بهینهسازی میشویم. البته هر چیز زیبایی در ریاضیات به کار بازار و اجرا نمیخورد؛ برعکس این موضوع هم درست است: چه بسیار کاربردها که برای علم زیبایی ندارد.
در سرتاسر تاریخ ریاضیات، همواره این علم رابطهی نزدیکی با مالی داشته است: از بابلیها شروع کنید تا تالس[۶]، فیبوناچی[۷]، پاسکال[۸]، فرما[۹] و تا برنولی[۱۰]، باشلیه، وینر[۱۱]، کولموگروف[۱۲]، ایتو[۱۳] و مارکوتیز[۱۴]، بلک[۱۵]، شولز[۱۶]، مرتن[۱۷] و بقیه.
بخش قابلملاحظهای از ریاضیدانان این فهرست، در توسعهی نظریههای خود به «مالی» توجه نداشتند، بلکه در پی توسعهی حوزهی ریاضی و احتمالات موردعلاقهی خود بودند. اما در دهههای بعد، از دستاوردهای آنان در توسعهی علم مالی ریاضی و مدلهای مالی استفاده شد. مثلاً پاسکال در توسعهی نظریهی احتمالات طبعاً کمتر به کاربرد مالی و اقتصادی آن علم توجه داشت، اما سالهای بعد، علم احتمالات به طور کامل در خدمت بسط علم اقتصاد و مالی قرار گرفت. از دورهی باشلیه است که نظریههای مالی ریاضی در سطح دانشگاهی شکل میگیرد و حتی در دانشگاهها فراموش میشود، و از زمان مارکویتز است که مالی ریاضی در میدان اجرا به کار گرفته میشود و توجه کسبکارهای مالی به این عرصه جلب میشود.
۳. نقش ریاضیدانان در عرصهی مالی
۳/۱. مهندسی مالی تالس
تالس در گذشتهای به دوری قبل از میلاد به دنیا نشان داد که اگر فیلسوفان هم بخواهند، میتوانند ثروتمند شود، اما آنان هدف دیگری را در زندگی دنبال میکنند. وی در زمستان یکی از سالها پیشبینی کرد که فصل برداشت زیتون مناسبی در راه است و براساس پیشبینی برداشت فراوان زیتون، همهی دستگاههای پرس زیتون را اجاره کرد و در زمان برداشت آنها را اجارهی مجدد داد، و سود عمدهای بدست آورد. بدینترتیب، طالس بدون آنکه بداند اولین قرارداد اختیار خرید[۱۸] را شکل داد.
۳/۲. فیبوناچی، مؤلف اولین کتاب مهندسی مالی
با نوشتن کتاب محاسبات[۱۹]، لئوناردو فیبوناچی عملاً اولین کتاب مهندسی مالی تاریخ را مینویسد. محاسبهی ارزش فعلی جریانهای نقدی بدیل، محاسبهی نرخ بازده و حل انواع مسائل غامض نرخ بهره همچون مثالهای پیچیدهای از قسطالسنین و مستمری دائمی در این کتاب به شرح درمیآید. او در عین حال قانون قیمت واحد را نیز تدوین کرد: «اگر دو دارایی جریان نقدی مشابه داشته باشند، میباید قیمت واحد داشته باشند.»
مباحث این کتاب در مورد بهره و جریان نقدی در اجرا به توسعهی نظام اعتباری و بانکداری در اروپا کمک کرد.
۳/۳. جیرلامو کاردانو و کتاب بازیهای شانس
کتاب بازیهای شانس[۲۰] جیرلامو کاردانو[۲۱]، این ریاضیدان دورهی رنسانس ایتالیا، براساس علاقهی وی به قمار و شرطبندی انتشار یافت. او در این کتاب نظریهی اولیهی شرطبندی را تدوین کرد و اصول بازی عادلانه[۲۲] را که گام نخست برای درک مارتینگل[۲۳] و فرضیهی ولگشت[۲۴] است، ترسیم کرد.
قمار و بیکاری وقت او را پر نمیکرد، و از اینرو دست به تنظیم اندیشههای خود زد و توانست به قواعد اولیهی احتمالات دست یابد و آنها را در کتاب خود توضیح دهد.
اصل اساسی در قمار، شرطبندی با شرایط یکسان و عادلانه است؛ شرایط یکسان بازیگران، تماشاچیان، پول، جعبهی طاس، و خود طاس. اگر از این شرایط عادلانه به نفع رقیب دور شویم، برای ما احمقانه است و اگر به نفع خودمان این اتفاق بیفتد، فرد عادلی نیستیم.
۳/۴. بلیز پاسکال[۲۵] و پیر دوفرما[۲۶] و طرح مسئلهی شوالیه دومِر[۲۷]
یک قرن بعد از کاردانو دو ریاضیدان فرانسوی به نامهای بلیز پاسکال و پیردوفرما راهحلی برای مسئلهای که شوالیه دومر (نجیبزادهی فرانسوی علاقهمند به قمار) طرح میکند، پیدا کرده و از آن طریق اولین مبانی نظریهی احتمالات را پایهریزی میکنند.
مسئلهی شوالیه دومر سودآوربودن شرطبندی روی جفت شش در ۲۴ پرتاب طاس است. آنان این مسئله را حل میکنند و در فرایند حل آن مبانی اولیهی نظریهی احتمالات را پی میریزند. آنان همچنین فرمول اولیهای برای قیمتگذاری مشتقهها طراحی میکنند.
۳/۵. خانوادهی برنولی و توسعهی مفاهیم مالی
در شروع قرن ۱۸، خانوادهی برنولی سوئیسی سهم بزرگی در نظریهی احتمالات بازی میکنند. ژاکوب برنولی[۲۸] اثبات اولیهی قانون اعداد بزرگ را برعهده داشت. این قانون میگوید اگر همان آزمایش را به تعداد بسیار زیاد تکرار کنید، آنگاه میانگین مشاهدهشده به سمت میانگین موردانتظار میل میکند. از این قانون مفهوم بسیار جالبی استخراج میشود؛ بدینترتیب مفهوم ارزش موردانتظار در «مالی» گیرمان میآید. بنابراین ژاکوب برنولی نقش عمده در توسعهی نظریهی احتمالات دارد و با اثبات اولیهی قانون اعداد بزرگ، به خلق مفهوم ارزش موردانتظار[۲۹] در مالی کمک میکند.
مدتی بعد دانیل برنولی[۳۰] گام بزرگی در جهت تدوین نظریهی ریسک در کتاب خود برمیدارد و در آن کتاب پارادوکس سنت پیترزبورگ را میشکافد. او با طرح مثالی از عموزادهی خود به بازیای اشاره میکند که در آن به متغیری تصادفی با ارزش موردانتظار نامحدود میرسیم که هر قمارباز منطقی با پرداخت قیمت محدودی وارد آن میشود. اما بازی ارزش بسیار کوچکی دارد و برای هر بازیگر منطقی، به دلیل ارزش موردانتظار آن، همین ارزش کوچک مطلوب خواهد بود. بدینترتیب دانیل برنولی این پارادوکس را با معرفی تابع مطلوبیت لگاریتمی حل میکند و به مفهوم مطلوبیت نهایی کاهشی میرسد که در اقتصاد زیاد با آن کار میکنیم. این دیگر ملاک قیمت نیست، بلکه مطلوبیت است که ارزش را تعیین میکند. برای اولینبار با این معیار تصمیمات سرمایهگذاری براساس نوعی مطلوبیت ارزیابی میشود که دیگر مطلوبیت خطی نیست.
بدینترتیب دانیل برنولی با توسعهی نظریهی ریسک و معرفی تابع لگاریتمی مطلوبیت و خلق مفهوم مطلوبیت نهایی کاهشی به رشتهی اقتصاد و مالی کمک میکند.
۳/۶. لوئی باشلیه و خلق پایههای نظریهی مالی نوین
پایاننامهی باشلیه با عنوان نظریهی سفتهبازی انقلابی در روند توسعهی علم مالی ایجاد میکند که ۶۰ سال ناشناخته باقی میماند. او در این پایاننامه هم به کاربرد ریاضیات حرکت براونی برای مدلسازی قیمتها در بازار سهام اشاره دارد، هم برای محاسبهی قیمت اختیار معامله راهحل معرفی میکند ﴿راهحلی که نتایج مدل باشلیه را با مدل بلک/ شولز/ مرتن بسیار نزدیک میکند﴾، و هم پایههای توسعهی نظریهی بازار کارا را استوار میکند.
آنچه به آن مالی مدرن میگوییم پدیدهی دهههای ۵۰ و ۶۰ قرن بیستم است. در این دو دهه است که تحولاتی در مالی شرکتها[۳۱] رخ میدهد؛ یعنی در مالی شرکتهای غیرمالی. اما تحول اساسی در مدلسازی ریاضی در حوزهی سرمایهگذاری و بازارهای سرمایه رخ میدهد؛ وقتی در «مالی» میگوییم «سرمایهگذاری[۳۲]»، منظورمان سرمایهگذاری در داراییهای مالی (اوراق بهادار) است.
مدل مارکوتیز (۱۹۵۲،۱۹۵۹)، مدل شارپ ۱۹۶۴، مدل لینتر[۳۳] ۱۹۶۵، مدل فاما[۳۴] ۱۹۶۵، مدل کندال[۳۵] ۱۹۵۳، مدل فیشر لوری[۳۶] ۱۹۶۵، مدل جنسون[۳۷] ۱۹۶۸ و بسیاری مدلهای دیگر همه و همه حاصل همان سالهاست.
با ذکر نام لوئی باشلیه در واقع اینجا تازه میرسیم به کسی که میتوانیم بگوییم شناسنامهی مالی ریاضی مدرن است و تازه چون خود او سالها بعد توسط ساموئلسون[۳۸] کشف میشود، عملاً مالی قبل از باشلیه چیزی نبوده، مگر مطالبی توصیفی.
باشلیه در پایاننامهی نظریهی سفتهبازی، اولین فردی است که از ریاضیات حرکت براونی (رابرت براون[۳۹]– گیاهشناس اسکاتلندی) برای مدلسازی حرکت قیمتها در بازار سهام استفاده میکند و از همانجا نیز راهحلی برای محاسبهی قیمت اختیار معامله ارائه میدهد. کار پیشتاز او در مورد عملکرد بازارهای مالی به توسعهی چیزی انجامید که امروزه فرضیهی بازار کارا به آن میگویند و نظریههای مرتبط با آن مثل مدل قیمتگذاری داراییهای سرمایهای[۴۰] بعدها شکل میگیرد.
مبدأ بیشتر آنچه بعدها، پس از اینکه در عمل به کار بسته میشود، مالی نوین[۴۱] نامیده میشود را میتوان به پایاننامهی لوئی باشلیه نسبت داد که در سال ۱۹۰۰ در سوربون از آن دفاع شد. این کار هم مبدأ و تولد مدل زمانپیوستهی ریاضیات فرایندهای تصادفی تلقی میشود و هم مدل زمانپیوستهی اقتصاد قیمتگذاری اختیارات. باشلیه دو اشتقاق از معادلهی دیفرانسیل جزئی فوریه به مثابهی معادلهای برای چگالی احتمالات بدست آورد؛ آنچه اکنون فرایند واینر/حرکت براونی نامیده میشود.
بعد از شناسایی قدرت تحلیل و توانهای بالای باشلیه، به افتخار او سالها بعد یعنی در سال ۱۹۹۶، جامعهی مالی باشلیه تأسیس میشود.
۳/۷. آندره کولموگروف[۴۲] و کتاب مبانی نظریهی احتمالات
یکی از نابغههای دنیای ریاضیات در کل تاریخ بشری است. کتاب مبانی نظریهی احتمالات وی نشان میدهد که احتمالات چیزی مرتبط با ریاضیات و در عین حال متفاوت با آن است او انداموارهای جدید برای نظریهی احتمالات مبتنی بر قضایای بنیادین ساخت و در واقع به طور کامل احتمالات را درون ریاضیات تعریف و با آن یکپارچه کرد. کولموگروف نه تنها سهم بزرگی در شکلگیری نظریهی احتمالات دارد، بلکه همچنین در عرضههای مکانیک آماری، فرایندهای تصادفی، نظریهی اطلاعات، دینامیک غیرخطی و آمار ریاضی کار کرده است.
همهی این مباحث کارکردهای عمدهای در مالی و ریاضیات دارد.
۳/۸. هنری لوبگ[۴۳] و مفهوم انتظارات تصادفی
طرح مفاهیم انتظارات تصادفی و سنجههای معادل که به ریاضیدانان مالی امکان داد فرمول برای قیمت مشتقهها بیابند، به لوبگ متعلق است.
هنری لوبگ و دیگران در آغاز قرن بیستم قضایای[۴۴] درستی برای احتمالات تعریف کردند که از آن طریق مفاهیمی چون انتظارات تصادفی و سنجههای معادل شکل گرفت و اینها همه خود راهی شد برای دستیابی به فرمولهای مختلف برای محاسبهی قیمت مشتقهها. بنابراین، در شکلگیری نظریهی قیمتگذاری مشتقهها که به دههی ۷۰ قرن بیستم میلادی برمیگردد، عدهی قابلملاحظهای مشارکت داشتهاند، هر چند که در زمان خود آن مطالعات چندان مورد توجه بازارهای مالی قرار نگرفت.
۳/۹. کیوشی ایتو[۴۵] و لِم مورد استفاده در مالی
کتاب دربارهی معادلات دیفرانسیل تصادفی معروفیت جهانی دارد. در این کتاب است که یکی از فرمولهای ریاضی که امروزه بسیار مورد استفادهی مهندسان مالی است و لم ایتو نامیده میشود، معرفی میشود. این عنوان از نام ریاضیدان ژاپنی کیوشی ایتو گرفته شده است. در نوشتهی با ارزش او دربارهی معادلات دیفرانسیل تصادفی، وی در تلاش است برای مدلسازی فرایندهای مارکوف، معادلات دیفرانسیل تصادفی را شکل دهد. لِم ایتو از معادلات ارائهشده به شکل جدیدی از معادلات دیفرانسیل تصادفی میرسد و عملاً ایتو پدر معادلات دیفرانسیل تصادفی شناخته میشود و پایههای حسابان تصادفی را میریزد.
در سخنرانی دریافت جایزهی کیوتو در ۱۹۹۸ وی وصف دلپذیری از زیبایی ریاضیات عرضه میکند «در ساختارهای ریاضی خوشساخت، ریاضیدانان همان زیبایی را مییابند که در قطعهی موسیقی دلنشینی و یا در شاهکار معماری یافت میشود. اما تفاوت بزرگی بین زیبایی ساختارهای ریاضی و آن هنرها وجود دارد. برای مثال، موسیقی موتزارت تا حد زیادی حتی کسانی را که نظریهی موسیقی را نمیدانند، تحتالشعاع و تأثیر قرار میدهد و کلیسای جامع کلن بینندگان را بشدت متأثر میکند، حتی اگر چیزی از مسیحیت نمیدانند. اما زیبایی در ساختارهای ریاضی بدون درک گروهی از فرمولهای ریاضی که بیانگر قوانین منطق است، دریافت نمیشود. تنها ریاضیدانان میتوانند «خط و ربطهای موسیقیایی نهفته در فرمولهای عددی متعدد را بخوانند و آن “موسیقی” را در دل خود بنوازند. از اینرو معتقدم بدون فرمولهای عددی، نمیتوانم ملودی زیبایی را که در جان من نواخته میشود، به دیگران انتقال دهم. وقتی اول بار معادلات دیفرانسیل تصادفی را شرح دادم، مقالهی من چنگی به دل کسی نزد؛ ده سال بعد بود که دیگر ریاضیدانان شروع به خواندن خط و ربطهای موسیقیایی من کردند و امروز در حال نواختن موسیقی من با سازهای خود میباشند.»
آنچه کیوشی ایتو در مورد تفاوت ساختار ریاضی با ساختارهای هنری یادآور میشود، به آن معناست که ریاضی در محدودهی فهم عامه و شعور عمومی توسعه نمییابد. واقعیت مشابه آن است که اقتصاد و مالی هم در چارچوب شعور عمومی شکل نگرفته و توسعه نمییابد. زیبایی ملودی اقتصاد تنها در دل اقتصاددانان و با سازهای آنان نوای خوشالحانی دارد.
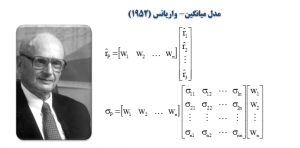
۳/۱۰. هری مارکوتیز و گزینش سبد اوراق بهادار
با نام هری مارکویتز است که مالی عملاً به سمت مالی ریاضی پیش برده میشود. مارکویتز همزمان با ایتو مقالهی گزینش سبد اوراق بهادار[۴۶] را نوشته است. اولین نوشتهی با نفوذ در مالی ریاضی که خارج از دانشگاه نیز توجهها را به خود جلب میکند. در این مقالهی سال ۱۹۵۲ و سپس کتاب ۱۹۵۹ وی که در آن مبانی متنوعسازی کارآمد را توضیح میدهد، مارکویتز پایهی چیزی را میگذارد که امروز به آن نظریهی مدرن سبد اوراق بهادار[۴۷] میگویند. قبل از وی، سرمایهگذاران سبد اوراق بهادار خود را با ارزیابی ریسک و بازدهی تکتک سهام انجام میدادند و بنابراین سبدی میساختند که ویژگیهای ریسک و بازده مشابه داشت.
بحث مارکویتز آن بود که سرمایهگذاران میباید سبدهایی بسازند که ویژگیهای ریسک بازده کلی داشته باشد؛ وی این کار را با محاسبهی میانگین بازده و واریانس برای سبد معین انجام داد. وی مفهوم مرز کارایی را معرفی کرد که ارائهی تصویری آن به نتایج مجموعهای از سبدهایی اشاره دارد که بالاترین نرخ بازده را برای سطح ریسکهای مختلف نشان میدهند.
این مفاهم راه را برای جیمز توبین باز کرد که سبد اوراق بهادار بسیار کارا وخط بازار سرمایه را معرفی کند و برای ویلیام شارپ این امکان را پدید آورد که مدل قیمتهای داراییهای سرمایهای CAPM را تدوین کند. خط بازار سرمایهی توبین امکان تشکیل سبدهای کارآمدی را روی خط بازار سرمایه نشان میدهد که ترکیبی از شاخص بازار و وامدهی یا وامگیری است. مدل شارپ نیز مبتنی بر نظریهی مارکویتز مدل سادهای را تدارک میبیند که به اتکای آن داراییهای سرمایهای قابل قیمتگذاری میشود.
بدینترتیب در نتیجهی مطالعات مارکویتز امکان تشکیل سبد، امکان انجام محاسبات میانگین بازده و واریانس سبد، تعیین مرز کارایی، و ارائهی راهحل برای بهینهسازی ریاضی ممکن شد.
این مطالعات در کنار اعطای جایزهی نوبل اقتصاد به مارکویتز، جایزههای متعدد دیگری و از جمله جایزهی انجمن تحقیقات عملیاتی را نصیب وی کرد. چنین ترکیبی از جوایز بیانگر آن است که این محقق و استاد اقتصاد در حوزهی ریاضیات و پژوهشهای کمّی مبسوطالید است.
مارکویتز همچنین نحوهی حل مسائل از طریق بهینهسازی ریاضی را ارائه کرد. مدلهای کامپیوتری برای شبیهسازی ساخت و در کنار جایزه نوبل در اقتصاد جایزه انجمن تحقیقات در عملیات را دریافت کرد که جایزهای ریاضی بود.
۳/۱۱. فیشر بلک، مایرون شولز و رابرت مرتن و مدل قیمتگذاری اختیار خرید
در سال ۱۹۷۳ که بلک و شولز مقالهی «قیمتگذاری اختیار معامله و تعهدات شرکتها» را انتشار دادند، انقلابی در رشته مالی رخ داد. این مدلی برای قیمتگذاری اختیارهای Put و Call اروپایی بود. همزمان بورس اختیار معاملهی شیکاگو شکل میگیرد تا اختیارهای فهرست شده را معامله کند و عملاً فرمول بلک و شولز تبدیل به وسیلهی کار کارگزاران میشود. قبل از ۱۹۷۵، همهی کارگزاران سبدهای اختیار معاملهی خود را براساس مدل بلک شولز (که در ماشین حسابهای خود تعبیه کرده بودند) ارزیابی میکردند و بر آن اساس ریسکپناهی[۴۸] را انجام میدادند. بعدها مرتن در تدقیق فرمول به شولز کمک کرد. البته کار آنها و بهویژه فیشر بلک محدود به اختیار معامله نبود و در حوزههای مختلف چون قیمتگذاری بدهی شرکتها، ساختار ریسک نرخهای بهره، روشهای نوین قیمتگذاری داراییهای مالی، قیمتگذاری اختیار معاملهی خرید و فروش اروپایی، و مدلسازی شبیهسازی تحقیق کردهاند.
به دلیل نقش عمده در توسعهی ادبیات ریاضی مالی، جایزهی نوبل در اقتصاد به شولز و مرتن تعلق گرفت. در آن زمان فیشر بلک فوت شده بود.
۳/۱۲. تحقیقات گستردهی منشعب از تحقیقات فیشر بلک/ مایرون شولز و مرتن
تحقیقات وسیعی ریشه از تحقیقات فیشر بلک، مایرون شولز و مرتن گرفته و برپایهی کار آنان شکل میگیرد. مفهوم اساسی در این تحقیقات مفهوم «نیکویی» یا «استواری[۴۹]» است. استفاده از این واژه در اقتصاد مربوط به پایداری[۵۰] مدلهای اقتصادی تحت فرضیات مختلف و پارامترهای مختلف است. چقدر سیستمهای اقتصادی در بازارهای مختلف و شرایط مختلف بازار مؤثراند و پایداری دارند؟
دو برندهی جایزهی نوبل پیتر هنسن[۵۱] و توماس سارجنت[۵۲] با نوشتن کتابی با عنوان استواری تکنیکهای کنترل پایدار با کاربردهای متنوعی از مسائل در اقتصادهای کلان پویا ارائه دادند.
بدینترتیب استواری دارد به مفهومی برجسته در اقتصاد تبدیل میشود که زمینهی ریاضی قوی میخواهد. در مالی ریاضی این مفهوم نخست در شکل «قیمتگذاری استوار» و «ریسکپناهی اختیار معاملهها» بروز کرد.
۳/۱۳. یوجین فاما و نظریهی بازار کارا
از مفهوم نظریهی بازار کارا (۱۹۷۰) برای مطالعات تجربی در زمینهی قیمتگذاری دارایی گسترده استفاده میشود. فاما خود به عنوان مبدع نظریهی بازار کارا (البته مبتنی بر نقطهنظر متقدمینی که در این خلاصه شرح کوتاهی از آنان ارائه شد) منتقد این نظریه هم هست. این اقتصاددان مالی ریاضی در حوزهی نظریهی سبد اوراق بهادار و قیمتگذاری داراییهای سرمایهای نیز کار کرده است و نهایتاً موفق به کسب جایزهی نوبل شده است.
در این مطالعه کوتاه از رابطهی متقابل ریاضیات و مالی، به نقش کامپیوتر نپرداختیم. به علاوه، تحلیلهای مبتنی به دادههای بزرگ یا big data در این سخنرانی کوتاه نیامد و طبعاً از نقش اقتصاددانان ریاضی درون شرکتها چیزی گفته نشد، چرا که مدلهای آنان بر ما ناشناخته باقی مانده است.
*. متن سخنرانی حسین عبده تبریزی در پنجمین همایش ریاضیات و علوم انسانی، در محل دانشکدهی اقتصاد دانشگاه علامهی طباطبایی، که از نوار استخراج و با اصلاحات اندک مکتوب شده است
[۱]. quants
[۲]. finance
[۳]. Bachelier
[۴] . McCulley
[۵]. duration
[۶]. Thales
[۷]. Fibonacci
[۸]. Pascal
[۹]. Fermat
[۱۰]. Bernoulli
[۱۱]. Wiener
[۱۲]. Kolmogorov
[۱۳]. Ito
[۱۴]. Markowitz
[۱۵]. Black
[۱۶]. Scholes
[۱۷]. Merton
[۱۸]. call option contract
[۱۹]. Liber Abaci
[۲۰]. Liber de Ludo Aleae
[۲۱]. Girolamo Cardano
[۲۲]. fair game
[۲۳]. martingale
[۲۴]. random walk hypothesis
[۲۵]. Blaise Pascal
[۲۶]. Pierre De F Ermat
[۲۷]. Chevalier De Mere
[۲۸]. Jacob Bernoulli
[۲۹]. expected value
[۳۰] . Daniel Bernoulli
[۳۱]. corporate finance
[۳۲]. investment
[۳۳]. Lintner
[۳۴]. Fama
[۳۵]. Maurice Kendall
[۳۶]. Fisher-Lorie
[۳۷]. Jensen
[۳۸]. Samuelson
[۳۹]. Robert Brown
[۴۰]. Capital Asset Pricing Model (CAPM)
[۴۱]. modern finance
[۴۲]. Andrey Kolmogorov
[۴۳]. Henri Lebesgue
[۴۴]. axiom
[۴۵]. Kiyoshi Ito
[۴۶]. portfolio selection
[۴۷]. Modern Portfolio Theory یا MPT
[۴۸]. hedging
[۴۹]. robustness
[۵۰]. sustainability
[۵۱]. Peter Hansen
[۵۲]. Thomas Sargent